我常常听到人们讲,是由于不雅观察者通过光子和电子发生相互浸染使光子的动量受到了影响,以是才导致了海森堡不愿定性事理。
不雅观察者必须通过影响电子的动量(或一些量子态)来不雅观察它,这或许是真的,但这不是导致不愿定性事理的真正缘故原由!

在开始谈论这个话题之前,让我们先定义海森堡不愿定性事理(Heisenberg’s uncertainty principle)。
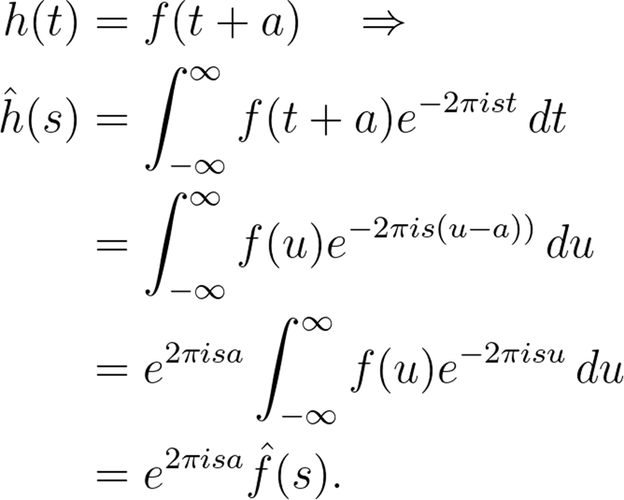
在量子力学中,存在一系列关于共轭物理量(如位置和动量)的不等式,它们限定了同时丈量这些成对物理量的精度,这些不等式中的任意一个都可以被称为不愿定性事理(或是海森堡不愿定性事理)。
-维基百科
一种常见的表述办法是,在任何给定的韶光点,你都无法同时准确地丈量粒子的动量和位置。
这种不愿定性不取决于设备的好坏,也不是由于很难肃清丈量偏差。无论我们做得多好,我们都无法同时精确丈量这两个量(如动量和能量)…
首先,存在许多种不愿定性事理,个中不少能在宏不雅观天下中看到。纵然你没故意识到它们的存在,但实在也一贯在和这些征象打交道。
其次,海森堡不愿定性事理背后与数学有着密切的关系。
所有波和物质(共轭变量)都必须屈服一系列的不愿定性事理,真正导出这些事理的是一个数学事实(稍后详述)。
音乐、雷达技能、能源技能和光也有必须遵守的“不愿定性事理”,我们很快就会看到,是数学决定了这统统。
波
统统都可以归结为非常大略的事情。无论多繁芜的的旗子暗记或函数,实际上都是正弦波的叠加。正弦波是具有特定波长和振幅的波。
叠加仅仅意味着所有的波相互浸染,所有波的和(称为干涉)便是构成更繁芜旗子暗记的叠加。
也便是说,我们可以将一个函数分解为组成它的更大略的部分(正弦波)。这险些便是我们在打算傅里叶级数的傅里叶系数时所要做的统统。值得的一提的是,这个方法对付非周期函数同样适用。
这种效果在音乐中是众所周知的,例如,吉他生中的泛音会滋扰主波(弦的频率)。也便是说,吉他的声音(以及任何其他乐器,包括你的声音)是由频率和振幅不同的正弦波组成的。
当我们描述这样一个繁芜的旗子暗记时,我们有两种等价的办法可以选择。也便是说,我们可以选择两种不同的单位对它进行描述。
我们可以选择用韶光来描述产生干涉图样的所有波是如何同时相互浸染的,也可以选择用构成干涉图样的正弦波的频率来描述它。
可以用两种等效的办法来描述的事宜被称为双重关系(dual relationship)。
如果我们可以找到一个数学工具来描述韶光旗子暗记和频率旗子暗记之间的双重关系,那当然再好不过。事实上,我们确实找到了这样的工具。
傅里叶变换
我上面提到的描述这种双重关系的工具叫做傅里叶变换(Fourier transform)。毫无疑问,它是数学工具中最强大、最常用的工具之一。
在给出它的一些特性之前,我们先讲一讲这种傅里叶变换的一些一样平常性子:
傅里叶变换是一种积分变换(也便是一个算符),它拿到一个函数并返回另一个函数。
作为函数空间上的一个算符,我们可以把它看作是纯数学的客体,但我们可以授予它很好的物理解释。在物理和数学领域,我们都可以利用它。
本日,我们紧张将从物理学的角度来考虑它。
不才面的谈论中,我们假设积分始终收敛。
令
是一个可积函数。f的傅里叶变换由以下积分给出:
如果f表示声波随韶光的变革,那么f傅里叶变换的结果表示构成声波的频率,因此f也可以看做是频率的函数。
下面的动图显示了声波(图中是单位脉冲旗子暗记)是如何由许多正弦波组成的,正弦波的叠加产生了sinc函数,即
理解旗子暗记总是可以用两种等效的表达办法是非常主要的。只要给定个中一个,另一个是唯一确定的,我们有一个公式可以对它们进行打算。如何选择仅仅取决于我们想用什么办法表达一个旗子暗记。
唯一的傅立叶逆变换由以下公式得出:
傅里叶变换的性子
傅里叶变换不是一两节课就可以讲清楚的,我们只能在本文中讲点皮毛。然而,傅里叶变换的一些令人惊奇的特性是一定要讲的:
首先是平移的影响。假设
通过变量的变换,我们得到:
韶光平移(旗子暗记延迟)会让频率函数产生一个相位移动。那变量的缩放会产生什么影响呢?
假设
我们将分别从a<0和a>0进行谈论。
个中利用了代换u=at。让我们看看当a<0时会发生什么:
进一步我们得到表达式:
它的物理意义是什么?
傅里叶变换的标度特性意味着,如果我们在韶光上压缩旗子暗记,相称于在频率空间(水平)上扩展旗子暗记,反之亦然。
我们很快就会创造,这一结果极其主要。
通过维度进行剖析可以给我们供应一个更高层次和有启示性的视角。韶光以秒为单位衡量,频率以1/s为单位进行衡量。彷佛可以看出,如果把韶光展宽变大,频率展宽就会变小,反之亦然。
如果你不知道频率的单位是从哪里来的,我非常能理解你的迷惑。傅里叶变换中的s终极决定了构成旗子暗记的正弦波的周期,你可以通过利用欧拉公式将复指数展开为正弦和余弦,或者将傅里叶变换视为一组连续的傅里叶系数来感想熏染这一点。
傅里叶变换有很多炫酷的特性,但由于这不仅仅是一篇关于变换本身的文章,我们将不过多先容这些特性,感兴趣的读者可以自己来探索这一点。
读者可能会创造一个让打算变简便的特性,即傅里叶变换将求导数转换为乘以一个常数,这是一个有趣且具有实用代价的特性。这意味着一个空间中的微分方程对应于另一个空间中的代数方程。
因此,一些微分方程可以通过变换方程,用代数方法求解,然后将解变换回来(通过傅立叶逆变换)得到原来方程的解。
波函数和海森堡不愿定性事理
量子物理学家通过可能存在的量子态来描述量子系统(例如粒子)。
描述量子态的函数族被称为波函数,以位置坐标为变量的波函数的模平方给出了粒子在空间中的概率分布。
因此,我们可以将波函数阐明为概率波,表示粒子位于给定空间区域的概率。因此,描述粒子位置的波函数该当被看作是空间中的波而不是韶光中的波。
当我们对这个位置波(位置坐标为自变量的波函数)进行傅里叶变换时,可以得到一个频率(空间中的频率)波,它因此粒子动量为自变量的波函数。
仔细想想并不奇怪,由于如果你认为光是波包或物质波,那么动量将由光的频率给出。
我们用
和
来表示这种关系。个中γ是波长,h是普朗克常数,p是动量,f是频率,E是能量。
我们把一个粒子限定在越小的间隔内,位置波函数就越局域化(被水平挤压)。由于动量波函数是位置波函数的傅里叶变换,动量波函数将被水平拉伸,这意味着动量将有更大的不愿定性。这是之条件到的傅里叶变换的标度特性导致的。
事实上,这便是海森堡的不愿定性事理!
这里只有傅里叶变换起了浸染:
个中h是普朗克常数,Δx和Δp分别是位置和动量的不愿定性(标准差)。
普遍的不愿定性
当函数g是函数f的傅里叶变换时,我们称f和g为共轭变量或共轭对。事实上,对付任何共轭函数对,都存在不愿定性事理。
海森堡不愿定性事理只是共轭变量的特例。
从数学角度来看,为什么共轭变量的不愿定性事理成立?缘故原由是:短旗子暗记,如声音脉冲,须要许多频率不同的正弦波的叠加才能实现,只有许多特定频率的正弦波的叠加才能担保在一定范围之外波的振幅靠近于0。相反,旗子暗记越像正弦波,描述旗子暗记所需的频率就越少。
当你听到很短的一段声音时,你很难确定这段声音包含哪些频率;但如果你听到一段持续韶光很长的纯净旗子暗记,就能够区分出不同的频率。这也是不愿定性事理。
同样的,我们对雷达探测的目标的间隔知道得越多,对靠近或退却撤退的速率就知道得越少,反之亦然。这是多普勒和间隔的不愿定性。
还有其它许多共轭变量,它们都遵照各自的不愿定性事理,它们有一个共同点,那便是它们的成立都是有数学担保的!
波的数学只是限定了我们可以从某一量子态中获取多少信息。
海森堡不愿定性事理的影响真实存在
如果你把激光器对准狭缝,光屏会把部分光阻挡在外,对付穿透过去的一部分,接下来会发生神奇的事情。
光芒彷佛在狭缝后面的屏上扩散开来,如果你让狭缝变得更窄,那么光会弥散地更开。这彷佛和我们的直觉不一致?我们限定它的空间分布,它反而弥漫开来。
这个征象便是由海森堡不愿定性事理导致的。随着狭缝越来越窄,位置波(波函数)越来越局域化(窄),根据不愿定性事理,动量波函数的展宽越来越大,这使得越来越多方向的运动成为可能。
由于动量是一个有方向的矢量,这意味着光子在狭缝另一侧传播时弥散的角度变得越来越大,从而在屏上产生了俏丽的衍射图样。
不愿定性还可以阐明为什么太阳会发光,乃至可以阐明为什么霍金辐射的时空征象会让黑洞缩小。
我希望有一点明确:不愿定性是一种纯粹的数学征象,但由于量子系统让这些数学理论照进现实,因此不愿定性也可以被算作一种物理事理。
作者:Kasper Müller
翻译:Nothing
审校:zhenni
翻译内容仅代表作者不雅观点
不代表中科院物理所态度
编辑:zhenni










